On Subclasses of Bi-Univalent Functions Related to Quasi Subordination
Abstract
In this paper, we introduce and investigate two subclasses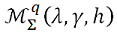 
and 
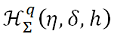of bi-univalent functions defined by quasi-subordination. We find estimates on the Taylor-Maclaurin coefficients 
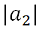and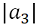 
for functions in these subclasses.
References
D.A. Brannan, J. Clunie and W.E. Kirwan, Coefficient estimates for a class of starlike functions, Canad. J. Math. 22 (1970), 476-485. https://doi.org/10.4153/CJM-1970-055-8
M.S. Robertson, Quasi-subordination and coefficient conjecture, Bull. Amer. Math. Soc. 76 (1970), 1-9. https://doi.org/10.1090/S0002-9904-1970-12356-4
Ch. Pommerenke, Univalent Functions, Vandenhoeck and Ruprecht, Göttingen, 1975.
S. Y. Lee, Quasi-subordinate functions and coefficient conjectures, J. Korean Math. Soc. 12(1) (1975), 43-50.
P.L. Duren, Univalent Functions, in: Grundlehren der Mathematischen Wissenschaften, Band 259, Springer-Verlag, New York, Berlin, Heidelberg and Tokyo, 1983.
F.Y. Ren, S. Owa and S. Fukui, Some inequalities on quasi-subordinate functions, Bull. Aust. Math. Soc. 43(2) (1991), 317-324. https://doi.org/10.1017/S0004972700029117
O. Altintas and S. Owa, Majorizations and Quasi-subordinations for certain analytic functions, Proc. Japan Acad. Ser. A 68(7) (1992), 181-185. https://doi.org/10.3792/pjaa.68.181
M.H. Mohd and M. Darus, Fekete-Szegö Problems for Quasi-subordination Classes, Abst. Appl. Anal. 2012 (2012), Article ID 192956. https://doi.org/10.1155/2012/192956
S. F. Ramadan and M. Darus, On the Fekete-Szegö inequality for a class of analytic functions defined by using generalized differential operator, Acta Universitatis Apulensis 26 (2011), 167-178.
S.P. Goyal and R. Kumar, Coefficient estimates and quasi-subordination properties associated with certain subclasses of analytic and bi-univalent functions, Math. Slovaca 65 (2015), 533-544. https://doi.org/10.1515/ms-2015-0038
P.P. Vyas and S. Kant, Certain subclasses of bi-univalent functions associated with quasi-subordination, J. Rajasthan Acad. Phys. Sci. 15 (2015), 315-325.
P. Sharma and R.K. Raina, On a Sakaguchi type class of analytic functions associated with quasi-subordination, Comment. Math. Uni. St. Pauli 64 (2015), 59-70.
R. El-Ashwah and S. Kanas, Fekete-Szegö inequalities for quasi-subordination functions classes of complex order, Kyungpook Mathematical Journal 55 (2015), 679-688. https://doi.org/10.5666/KMJ.2015.55.3.679
S.P. Goyal, O. Singh and R. Mukherjee, Certain results on a subclass of analytic and bi-univalent functions associated with coefficient estimates and quasi-subordination, Palestine Journal of Mathematics 5 (2016), 79-85.
N. Magesh, V. K. Balaji and J. Yamini, Certain subclasses of bi-starlike and biconvex functions based on quasi-subordination, Abstract and Applied Analysis, vol. 2016, Article ID 3102960, 6 pages. https://doi.org/10.1155/2016/3102960
T. Panigrahi and R. K. Raina, Fekete-Szegö coefficient functional for quasi-subordination class, Afr. Mat. 28(5-6) (2017), 707-716. https://doi.org/10.1007/s13370-016-0477-1
S. Altinkaya and S. Yalcm, Quasi-subordinations for certain subclasses of bi-univalent functions, Math. Adv. Pure Appl. Sci. 1(2) (2018), 56-64.
H.M. Srivastava, S. Hussain, A. Raziq and M. Raza, The Fekete-Szegö functional for a subclass of analytic functions associated with quasi-subordination, Carpathian J. Math. 34(1) (2018), 103-113.
D.A. Hussein, A.K. Wanas and S.J. Mahmood, Coefficient estimates for some subclasses of m-fold symmetric bi-univalent functions, Journal of Southwest Jiaotong University 55(3) (2020). https://doi.org/10.35741/issn.0258-2724.55.3.38
S. Yalçin, W. G. Atshan and H. Z. Hassan, Coefficients assessment for certain subclasses of bi-univalent functions related with quasi-subordination, Publ. Inst. Math. (Beograd) (N.S.) 108(122) (2020), 155-162. https://doi.org/10.2298/PIM2022155Y
D.A.H. Hussein and S.J. Mahmood, Coefficient estimates for some subclasses of m-fold symmetric bi-univalent functions defined by linear operator, Journal of Advances in Mathematics 20 (2021), 115-120. https://doi.org/10.24297/jam.v20i.8976
This work is licensed under a Creative Commons Attribution 4.0 International License.
.jpg){kind=logo}
