On Artin Cokernel of the Quaternion Group Q_{2m} when m=2^h \cdot p_{1}^{r_1} \cdot p_{2}^{r_2} \cdots p_{n}^{r_n} such that p_i are Primes, g.c.d.(p_i, p_j)=1 and p_i \neq 2 for all i = 1, 2, ..., n, h and r_i any Positive Integer Numbers
Abstract
In this article, we find the cyclic decomposition of the finite abelian factor group 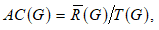
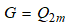
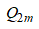
(The group of all Z-valued generalized characters of G over the group of induced unit characters from all cyclic subgroups of G).
We find that the cyclic decomposition 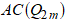
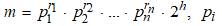
Moreover, we have also found the general form of Artin characters table 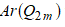
Downloads

This work is licensed under a Creative Commons Attribution 4.0 International License.
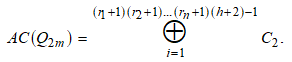
.jpg)
